工事担任者　取得の道しるべ
	『　電気気通信技術の基礎　』 ※非定期に加筆更新しています。　 　　　　　 　　　　　念のため，　　再読み込みをしてみてください！
	問題１の（１）直流回路　 　　　　　　　の既出設問パターンの概要把握と攻略研究	初版 2017/01/02 改版 2017/02/12
	攻略方法その１： 既出問題の分析 　平成２６年第１回　〜　Ｈ２８年第２回までの６回の既出問題を整理してみました 　　　　　使える基本的な実力？ 　　　　　　　　その１　　Ｅ ＝ Ｒ ・ Ｉ 　　・・・だけでなく電流の方向と電圧の向きの関係 　　　　　　　　その２　　直列抵抗の合成抵抗・・・・・　Ｒ＝Ｒ１＋Ｒ２・・・など 　　　　　　　　その３　　並列抵抗の合成抵抗 ・・・・　 1/（1/R1＋1/R2)など　 　　　　　　　　　　　　　　　　　　　・・・試験では暗算で計算できる数値が多用されてます　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　その４　　基本の基本を踏まえた上で， 　　　　　　　　　　　　　　　　あえて逆算的な答えの導き方も，実力の内！ 　　　　　　　　　　　　　　　　使わないという選択肢はないですね　・・・・・2017/02/11
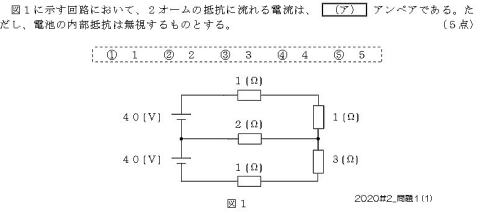
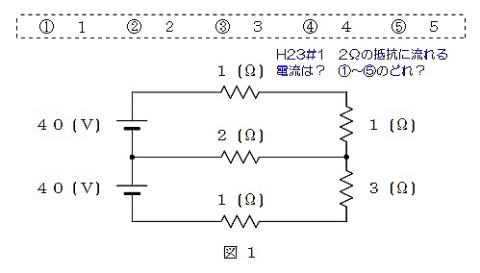
	２０２０(R02)#2問題１(1) 2011（Ｈ２３）＃１	【正攻法による解き方】 　　　連立方程式を立て，式を解く 　　　　　上側のLOOPを時計回りに流れる電流をＩ１ 　　　　　下側のLOOPを時計回りに流れる電流をＩ２ 　　　　　 と仮定 　　　　４０ ＝ Ｉ１×（１＋１）＋２×（Ｉ１−Ｉ2） ・・・・式１ 　　　　４０＋２×（Ｉ１−Ｉ2） = Ｉ２×（３＋１）　 ・・・・式２ 　　　　　　 　　　　この連立方程式が書ければ半分終わり。 　　　　　　式１は 　　　　　　　　　４０＝２Ｉ１＋２Ｉ１−２Ｉ２ 　　　　　　　　　４０＝４Ｉ１−２Ｉ２ 　　　　　　　　　　４Ｉ1＝４０＋２Ｉ２ 　　　　　　　　　２Ｉ１＝２０＋Ｉ２　・・・・・式１’　　　　　　　　　　　　　　　　 　　　　　　式２は 　　　　　　　　　　４０＋２Ｉ１−２Ｉ２＝４Ｉ２　 　　　　　　　　　　４０＋２Ｉ１−６Ｉ２＝０・・・・式２’ 　　　　　　式２’に式１’を代入 　　　　　　　　　　４０＋２０＋Ｉ２−６Ｉ２＝０　　　　　　　　　　 　　　　　　　　　　６０−５Ｉ２＝０ 　　　　　　　　　　　　 　５Ｉ２＝６０ 　　　　　　　　　　　　 　　Ｉ２＝１２ 　　　　　　式１’に　　Ｉ２＝１２を代入すると 　　　　　　　　　　２Ｉ１＝２０＋Ｉ２　　 　　　　　　　　　　２Ｉ１＝２０＋１２ 　　　　　　　　　　　　 ＝３２ 　　　　　　　　　　 Ｉ１＝１６ 　　　　　　答えは，Ｉ１−Ｉ２＝４（Ａ）
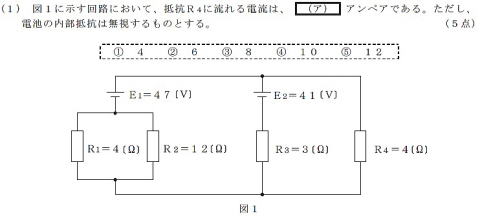
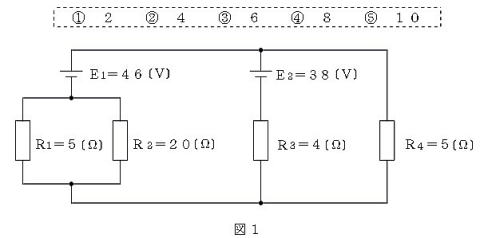
	2016（H28#1） このような，数値違いの例も 2019（Ｒ０１）#2　　　Ｒ４を流れる電流値を求める	H28#1　Ｒ４の電流？（Ａ）　　�@〜�D 【正攻法による解き方】 　　合成抵抗（並列）の計算・・・できれば暗算レベル 　　R12＝１/（1/4＋1/12） 　　　　 ＝1/（3/12＋1/12） 　　　　 ＝1/(４/１２） 　　　　 ＝12/４4 　　　 　＝ ３　 (Ω）　 　　電池電圧が異なるので， 　　ここは正攻法の連立方程式を解いて回答したい。 　　具体的解き方は市販参考書参考願います。 【逆算的な解き方】　 　　回答�@〜�Dの値を用い、 　　抵抗Ｒ４の端子電圧をＶＲ４を仮置きすると，ＩＲ３やＩＲ12 　　が算出できる。　　 4Ωの抵抗 端子電圧 3Ωの抵抗 電圧,電流 4Ωと12Ωの合成抵抗　R12 3Ω ＩＲ４ ＶR4 VR3 ＩＲ3 VR12 IR12 IR3+IR12 �@　４Ａ １６Ｖ 25V 25/3A 31V 31/3A 36/3A �A　６Ａ ２４Ｖ 17V 17/3A 23V 23/3A 40/3A �B　８Ａ ３２Ｖ 9V 3A 15V 5A ８Ａ �C１０Ａ ４０Ｖ １Ｖ 1/3Ａ 7V 7/3A 8/3A �D１２Ａ ４８Ｖ
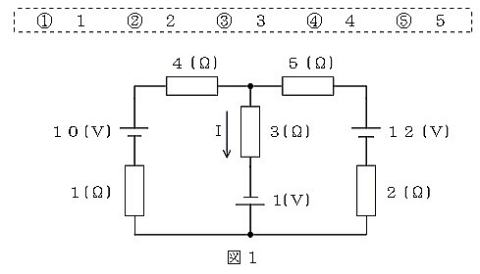
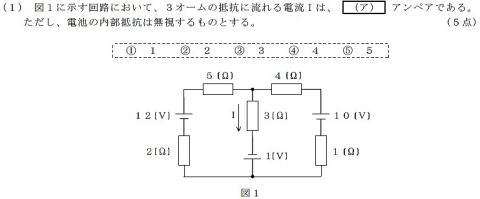
	2014（Ｈ２６）＃２ このような，数値違いの例も 2019（H３１）#1	H26#2　電流Ｉ（Ａ）は？ 【正攻法による解き方を推奨】 　 　正攻法の連立方程式を解いて回答したい。 　　具体的解き方は市販参考書参考願います。 【逆算的な解き方】 　　　これでも回答は可能 ３Ωの抵抗 ２Ω＋５Ω の抵抗 ４Ωと１Ω の抵抗 ＩＲ３ ＶR3 VR25 ＩＲ25 VR41 IR41 IR3＝ 　　IR25+IR41 �@　1Ａ ３V 10V 10/7Ａ 8V 8/5A �A　２Ａ ６Ｖ 7V １Ａ 5V 1A 合致 �B　３Ａ ９Ｖ 4V 4/7Ａ 2V �C　４Ａ 12V 1Ｖ 1/7A �D　５Ａ 15V 　　　　�@〜�DからVR3を埋める 　　　　VR25＝12V-VR3＋1V　　　⇒IR25 　　　　VR41＝10V-VR3＋1V　　　⇒IR41
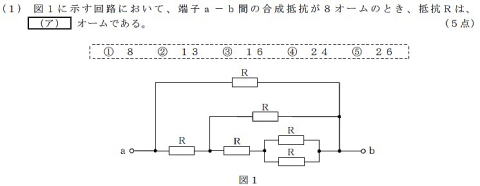
	H27(2015）＃１ H30（2018）＃２	H27#1 　　　　　端子ａ−ｂの合成抵抗値が８Ωのとき， 　　　　　　抵抗Ｒの値は？ 　　※サービス問題です・・・・1分前後で解きたい。 　　※正攻法による筆算での合成抵抗算出力は必須ですが， 　　　 その基礎力がある人は， 　　　　消去法による時短回答が可能です。　　 　　※端子ａ−ｂ間の合成抵抗は 　　　　　　抵抗Ｒより小さくなることに気付きます 　　　　　　　　よって　合成抵抗＝Ｒ　である　�@８Ωは誤り 　　　　　　次に， 　　　　　　合成抵抗は1/2Ｒよりわずかに大きいことも推察 　　　　　　できますね 　　　　　　　　よって　合成抵抗＝1/2Ｒ　である�Bは誤り 　　　　　　　　　　　　　合成抵抗＜1/2Ｒ　である�Cと�Dも誤り 　　　　　　残った�Aが答え！
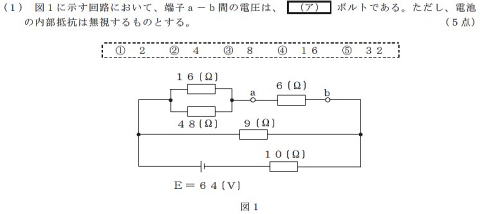
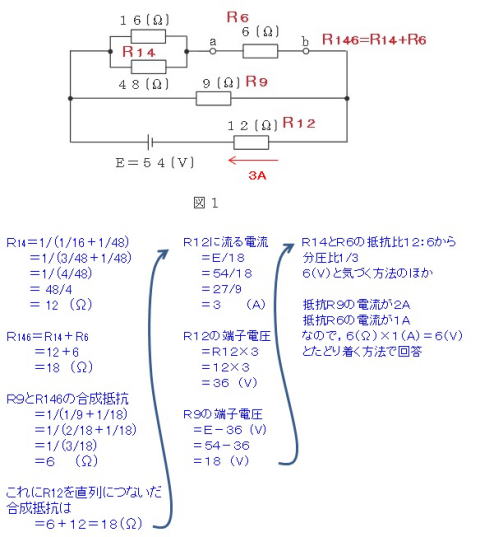
	H27（2015）＃２ H29（2017）＃２	H29年第2回 　（H27年第2回と回路は全く同じで， 　　　　　　　　　　　電池電圧のみ違います。） 　 　抵抗の並列接続した際の合成抵抗の計算 　抵抗を直列接続したときの合成抵抗計算 　全合成抵抗の算出 　電池電流の算出 　１２Ωの抵抗の端子電圧を求める力 　９Ωの抵抗の端子電圧を求める方法 　６Ωの　　　　〃　　　　　　求める方法 　といった基本的な知識を問う問題です。 　※余談ですが 　　　少し前まで暗算でスイスイと解けたのですが， 　　　加齢により怪しくなってきて， 　　　前に作った解説（暗算で・・・）に頭ががついて 　　　いけない自分に気づき愕然。 　　　今後は，より丁寧な解説に心がけしたいと思い 　　　はじめ，暗算で算出・・・という解説修正しはじめ 　　　ました（2020/12/26）。 　※問題用紙には， 　　　Ｒ１４の位置に，１２Ω 　　　Ｒ１４６の位置に１８Ω 　　　３Ａ 　　などと，適当な位置に 　　逐次，計算結果を明記していくことをお勧め 　　します。
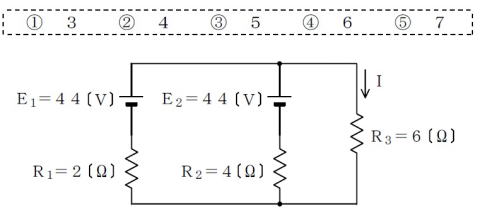
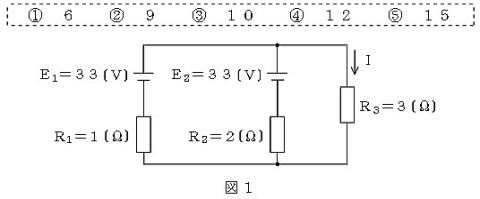
	2013（H25）#2-1(1) このような，数値違いの例も 2018（H30）#1	H25#2　電流 Ｉ　は何アンペア？　�@〜�D　からの択一 【正攻法による解き方】 　　　　　電池電圧が等しいことから，このように回路を 　　　　　簡略化 　　　　　　電池一個の先に，R1,R2の抵抗が並列に 　　　　　　接続されている回路に置き換えて考える。 　　　　　　Ｒ１，Ｒ２，Ｒ３の合成抵抗をＲ１２３とすると、 　　　　　　Ｒ１２３　＝ ６＋1/(1/2+1/4) 　　　　　　　　　　　＝６＋１/（（2+１)/4） 　　　　　　　　　　　＝６＋４／３ 　　　　　　　　　　＝（１８＋４）/３　 　　　　　　　　　　＝２２／３　　　　　（Ω）　　 　　　　　　Ｉ ＝　Ｅ１/R123 　　　　　　　＝ ４４×３／２２ 　　　　　　　＝　６　　　　（Ａ） 【逆算的な解き方】 　　　　Ｅ１＝Ｅ２に気付き 　　　　Ｒ１，Ｒ２，Ｒ３の電流の比率　　　　 　　　　　ＩＲ１：ＩＲ２：ＩＲ３＝２：１：３　　との直観で 　　　　答えを出してしまうことも可能だが， 　　　　下の表で各値を埋めても答えが見つかる。 Ｒ3　６Ω R１　２Ω R2　４Ω ＩＲ3 ＶR3 VR１ ＩＲ1 VR2 IR2 IR1+IR2 �@ ３A 18V 26V 13A 26V 26/4A �A ４A 24V 20V 10A 20V 5A �B ５A 30V 14V 7A 14V 14/4A �C ６A 36V 8V 4A 8V 2A ６Ａ 合致 �D ７A 42V ２Ｖ １Ａ ２Ｖ この場合は，正攻法の方が確実で早い回答ができるかも？
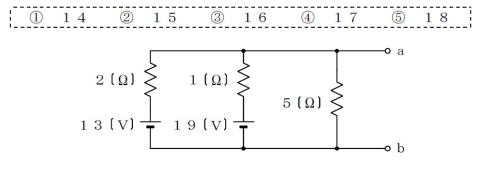
	2013（H25）＃１ 2017（H29）＃１	H25#１　端子ａ−ｂの電圧（Ｖ）を求める問題 【正攻法による解き方】 　　ここは正攻法の連立方程式を解いて回答したい。 　　具体的解き方は市販参考書参考願います。 【逆算的な解き方】 　　答�@〜�Dを見渡したときに， 　　　いずれも，１３Ｖの電池電圧よりも大きい。 　　　　　従って，２Ωの電流方向は，電池を充電する 　　　　　方向と判る。 　　　　　　IR1＝IR2+IR5　が成立する組み合わせを 　　　　　見つければよい。 ５Ωの抵抗 ２Ωの抵抗 １Ωの抵抗 ＶＲ5 ＩR5 VR2 ＩＲ2 VR1 IR1 �@　14Ｖ 14/5A 1V 1/2A ５V ５A �A　15Ｖ 3A 2V 1A ４Ｖ ４Ａ IR1＝IR2+IR5 �B　16V 16/5A �C　17Ｖ 17/5A �D　18Ｖ 18/5A 　　　↑5Ωの端子電圧�@〜�Dから2Ωおよび１Ωの電流 　　　　　を逆算し，題意に合致する�Aが答え。
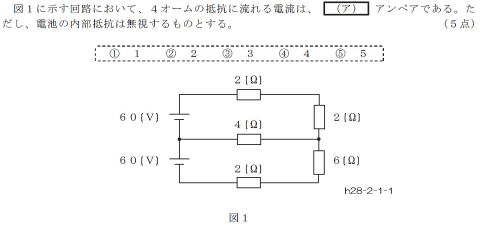
	H28#2-1(1) 　時短法解説	H28#２とH26#１で全く同じ問題が出ています。 　H28#2　中央の４Ωの抵抗に流れる電流？ 　H26#1　　　　同上 　 【正攻法による解き方】 　　　連立方程式を立て，式を解く 　　　　　上側のLOOPを時計回りに流れる電流をＩ１ 　　　　　下側のLOOPを時計回りに流れる電流をＩ２ 　　　　　 と仮定 　　　　60 ＝ Ｉ１×（２＋２）＋４×（Ｉ１−Ｉ2） ・・・・式１ 　　　　60＋４×（Ｉ１−Ｉ2） = Ｉ２×（６＋２）　 ・・・・式２ 　　　　　　 　　　　この連立方程式が書ければ半分終わり。 　　　　　　式１は 　　　　　　　　　６０＝４Ｉ１＋４Ｉ１−４Ｉ２ 　　　　　　　　　６０＝８Ｉ１−４Ｉ２ 　　　　　　　　　３０＝４Ｉ１−２Ｉ２　 　　　　　　　　　４Ｉ１＝３０＋２Ｉ２　・・・・・式１’　　　　　　　　　　　　　　　　 　　　　　　式２は 　　　　　　　　　　６０＋４Ｉ１−４Ｉ２＝８Ｉ２　 　　　　　　　　　　６０＋４Ｉ１−１２Ｉ２＝０・・・・式２’ 　　　　　　式２’に式１’を代入 　　　　　　　　　　６０＋３０＋２Ｉ２−１２Ｉ２＝０　　　　　　　　　　 　　　　　　　　　　９０−１０Ｉ２＝０ 　　　　　　　　　　　　　 １０Ｉ２＝90 　　　　　　　　　　　　 　　　Ｉ２＝9 　　　　　　式１’に　　Ｉ２＝9を代入すると 　　　　　　　　　　４Ｉ１＝３０＋２Ｉ２　　 　　　　　　　　　　４Ｉ１＝３０＋１８ 　　　　　　　　　　　　 ＝４８ 　　　　　　　　　　　 Ｉ１＝１２ 　　　　　　答えは，Ｉ1−Ｉ２＝３（Ａ）　 　　　 【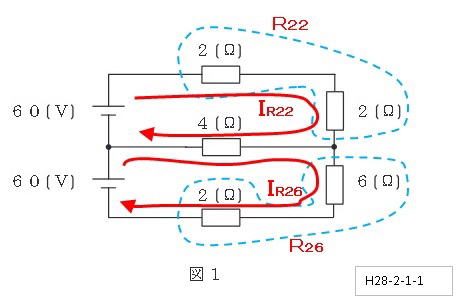時短法（逆算的な解き方）】 　　　・　４Ωの抵抗がないとき， 　　　 　 ２Ωと６Ωの接続点の電位が，電池同志の接続点より 　　　　　高いと気づくこと（必須ではないが） 　　　・　仮にＩＲ２２とＩＲ６２の電流を図示すること 　　　・　４Ωの電流値ＩR4は，二つの電池電流の相殺された 　　　　　差分（IR22-IR62）であること 　　　　　以上に気付けば　，�@〜�Dの答え順に， 　　　　　ＩR4＝IR22-IR62　となるものを探せばよい。 Ｒ4 ４Ωの抵抗 R22 2Ω＋2Ωの合成抵抗 R62 6Ω＋2Ωの合成抵抗 差分 ＩＲ4 ＶR４ VR22 ＩＲ22 VR62 IR62 IR22-IR62 �@ １A 4V 56V 14A 64V ８Ａ ６Ａ �A 2A 8V 52V 13A 68V 8.5A 4.5A �B 3A 12V 48V 12A 72V 9A 3A 合致 �C 4A �D 5A 　　　　　従って，答えは�B
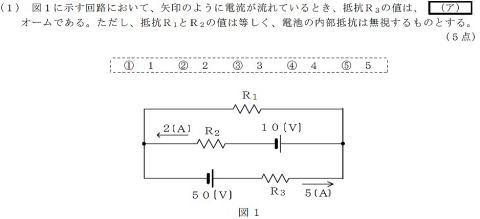
	2012（H24）#2　Ｒ３の抵抗値を求める	H24#2 　　電流の大きさと方向が明示されていることに着目 　　　　・Ｒ２の電流方向から， 　　　　　　　10Vの電池は充電方向であること 　　　　　　　50Vの電池電流の一部であること 　　　　　　　Ｒ１の電流は，差分の３Ａと判る。 　　　　・Ｒ１の端子電圧ＶＲ１は 　　　　　　　 　Ｒ１＝Ｒ２＝Ｒとした場合 　　　　　　　　ＶＲ１＝１０＋２×Ｒ 　　　　　　　　ＶＲ１＝３×Ｒ　　 　　　　　　　　　　　　　　⇒　Ｒ＝１０　Ω　，ＶＲ１＝30Ｖ 　　　　・Ｒ３の端子電圧ＶＲ３は 　　　　　　　　ＶＲ３＝５０−ＶＲ１＝２０Ｖ 　　　　　　　　Ｒ３　＝ＶＲ３/５ 　　　　　　　　　　　＝４　Ω
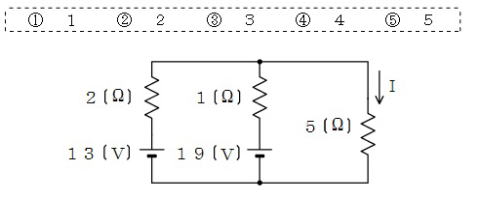
	2012（H24）#1　５Ωの抵抗電流を求める問題	【正攻法による解き方】 　　ここは正攻法の連立方程式を解いて回答したい。 　　具体的解き方は市販参考書参考願います。 【逆算的な解き方】 　　答�@〜�Dを見渡したときに， 　　�C�Dは，５Ωの端子電圧が電池電圧を超えるので× 　　 ５Ωの抵抗 ２Ωの抵抗 １Ωの抵抗 ＩＲ5 ＶR5 VR2 ＩＲ2 VR1 IR1 �@　1Ａ 5V 8V 4A 14V 14A �A　２Ａ 10V 3V 3/2A 9V 9A �B　３Ａ 15V ２Ｖ 1A充電 ４Ｖ 4A 合致 �C　４Ａ ２０Ｖ × �D　５Ａ ２５Ｖ × 　　　　�@〜�Dの値から　VR5を埋める

※記載内容に不明な点があった際は，下記メールアドレスまで，おしらせいただければ幸いです。
junklaboz　@yahoo.co.jp　　←スペースはつめてください　

著作権情報
初版　　　　　: 2016/12/29
最終更新日 : 2020/12/26
.